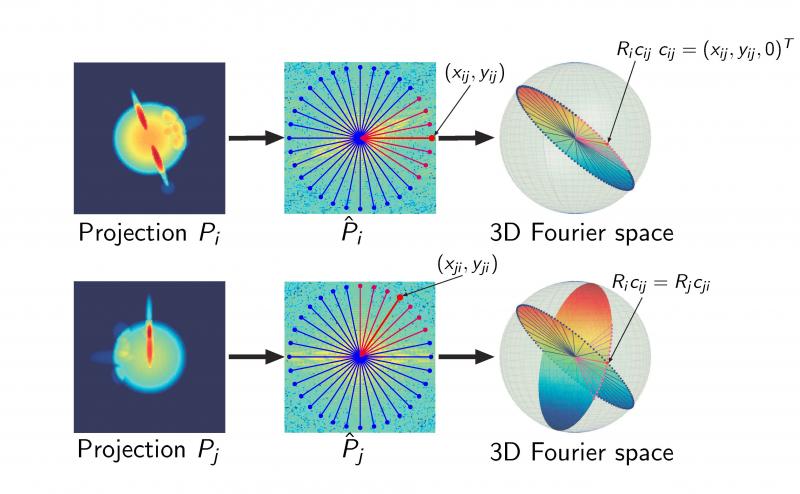
 The Fourier Projection Slice Theorem implies that the orientations of three projection images can be determined from their common lines, which is the foundation of the angular reconstitution method (van Heel 1987; Vainshtein and Goncharov 1986). The orientations of the remaining particles can be deduced in a sequential manner from their common lines with the previously orientation-assigned particles. However, conventional SPR algorithms fail with particles that are too small, with images that are too noisy, or at resolutions where the signal-to-noise ratio (SNR) becomes too small.
The Fourier Projection Slice Theorem implies that the orientations of three projection images can be determined from their common lines, which is the foundation of the angular reconstitution method (van Heel 1987; Vainshtein and Goncharov 1986). The orientations of the remaining particles can be deduced in a sequential manner from their common lines with the previously orientation-assigned particles. However, conventional SPR algorithms fail with particles that are too small, with images that are too noisy, or at resolutions where the signal-to-noise ratio (SNR) becomes too small.
Our toolbox provide several common-line based algorithms that utilize the information in the common lines between all pairs of images simultaneously, leading to an assignment of orientations that is as consistent as possible with the common lines. Our approaches use convex optimization and semidefinite relaxation, spectral methods and Bayesian approaches, and work for both uniform and non-uniform viewing angle distributions. It is recommended to use our orientation assignment algorithms on class averages rather than on the raw images whose SNR is typically too low. Our algorithms assume a non-symmetric molecule; In the future we plan to extend the algorithm to deal with molecules with non-trivial point-group symmetry.
Further reading:
L. Wang, A. Singer, Z. Wen, Orientation Determination from Cryo-EM images using Least Unsquared Deviations, SIAM Journal on Imaging Sciences, 6 (4), pp. 2450-2483 (2013). PMID:24683433 [PubMed] PMCID: PMC3966634.
Y. Shkolnisky, A. Singer, Viewing Direction Estimation in Cryo-EM Using Synchronization, SIAM Journal on Imaging Sciences, 5 (3), pp. 1088-1110 (2012). PMID: 24363820 [PubMed] PMCID: PMC3868463
A. Singer, Y. Shkolnisky, Three-Dimensional Structure Determination from Common Lines in Cryo-EM by Eigenvectors and Semidefinite Programming, SIAM Journal on Imaging Sciences, 4 (2), pp. 543-572 (2011). PMID: 22536457 [PubMed]; PMCID: PMC3334316.
R. Hadani, A. Singer, Representation theoretic patterns in three dimensional Cryo-Electron Microscopy I - The intrinsic reconstitution algorithm', Annals of Mathematics, 174 (2), pp. 1219-1241 (2011). PMID: 23180881 [PubMed] PMCID: PMC3505076.
A. Singer, R. R. Coifman, F. J. Sigworth, D. W. Chester, Y. Shkolnisky, Detecting Consistent Common Lines in Cryo-EM by Voting, Journal of Structural Biology, 169 (3), pp. 312-322 (2010). PMID: 19925867 [PubMed - indexed for MEDLINE] PMCID: PMC2826584.
R. R. Coifman, Y. Shkolnisky, F. J. Sigworth, A. Singer, Reference Free Structure Determination through Eigenvectors of Center of Mass Operators, Applied and Computational Harmonic Analysis, 28 (3), pp. 296-312 (2010). PMID: 20436952 [PubMed] PMCID: PMC2860334.
